Une fonction est dite nulle lorsque la valeur de « y » demeure toujours la même, peu importe la valeur de « x ». Voici un exemple sous la forme d’un graphique. Dans ce même graphique, on peu voir que « y » égale toujours 4. La règle est donc : y=4.
Bienvenue sur mon site internet sur les mathématiques de secondaire 3, j’espère que cela va vous être utile.
Les nuages de points sont des types de graphiques avec des points sur les données. On n’a pas besoin de tracer une ligne droite ou courbe. Voici un exemple. La ligne rouge représente la moyenne des données dans le plan cartésien.
Voici les sources que j’ai utilisé :
– http://bv.alloprof.qc.ca/mathematique/arithmetique/la-factorisation-des-nombres.aspx
– http://www.sylvainlacroix.ca/ESW/Files/306_ProprieteExposant.pdf
– http://fr.wikipedia.org/wiki/D%C3%A9composition_en_produit_de_facteurs_premiers
– http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Pythagore
– http://csap.ednet.ns.ca/pdf/Activite11_excel.pdf
– http://www.statcan.gc.ca/edu/power-pouvoir/ch9/scatter-nuages/5214827-fra.htm
Les ensembles de nombres sont les catégories dans lesquelles sont placés les nombres. Voici un graphique qui démontre bien ces catégories de nombres.
Naturel (IN) : Tous les nombres positifs entiers. Exemple : 1 et 10
Entiers (IZ) : Tous les nombres entiers positifs et négatifs. Exemple : -10 et 10
Rationnels (Q) : Tous les nombres qui peuvent s’écrire sous forme de fraction avec un numérateur et dénominateur. Exemple : 1/4 et 2,4 et 2 et -2/1
Irrationnels (Q’) : Tous les nombre qui ne peuvent pas être écrits sous forme de nombres périodiques. Exemple : π et √2
Réels (RI) : Tous les nombres. Exemple : 1 et -2 et 3,4 et 1/3 et π
Les systèmes d’équations sont des ensembles d’au moins 2 équations. En secondaire 3, nous touchons seulement aux systèmes d’équations linéaires. Cela consiste à trouver un point de rencontre entre deux fonctions.
Il y a trois réponses possibles lorsque l’on résout un système d’équations.
– Une solution unique : lorsqu’il y a un moment où les droites se croisent.
– Aucune solution : lorsque les droites sont parallèle
– Infinité de solutions : lorsque les droites sont sur la même ligne.
Voici un problème qui met en valeur les systèmes d’équations : Nicolas et Élodie calculent le nombre de casquettes qu’ils reçoivent. Nicolas reçoit 2 casquettes par semaine et il en a déjà 10. Élodie en reçoit 4 par semaine. Après combien de semaines, Élodie aura autant de casquettes que Nicolas.
1 – Identifier les variables
x : nombres de semaines
y : nombres de casquettes
2 – Établir les 2 systèmes d’équations
Nicolas (y1) = 2x + 10
Élodie (y2) = 4x
3 – Poser l’équation (trouver x donc le nombres de semaines pour qu’ils aient le même nombre de casquettes)
4x = 2x + 10
4x – 2x = 10
2x = 10
2x ÷ 2 = 10 ÷ 2
x = 5
Réponse : 5 semaines
Quand un applique un exposant, indique que l’on doit multiplier plusieurs fois par lui-même un nombre. Par exemple : 3^2 = 3*3 = 9. Quand l’exposant est 0, la réponse demeure toujours 1, peu importe le nombre. Exemple : 100000000^0 = 1. Voici les termes reliés à l’exposant :
Règle 1 : Lorsqu’on multiplie des nombres avec des exposants, il faut additionner les exposants.
3^2 * 3^5 = 3^2+5 = 3^7
Règle 2 : Lorsque l’on divise des nombres avec des exposants, il faut soustraire au première exposant la valeur du deuxième exposant.
3^7 ÷ 3^5 = 3^7-5 = 3^2
Règle 3 : Lorsque l’on multiplie deux exposant entre-eux, il faut multiplier les deux exposant.
(3^2)^3 = (3^2)^3 = 3^6
Règle 4 : Lorsqu’il y a une fraction avec un exposant, le dénominateur et le numérateur ont l’exposant.
(3/4)^2 = 3^2/4^2 = 9/16
Règle 5 : Les exposants négatifs peuvent devenir positifs. Il suffit de mettre le chiffre sous forme de fraction, inverser la base et de mettre l’exposant positif.
3^-3 = (1/3)^3 = 1^3/3^3 = 1/9
Tous les nombres peuvent s’écrire sous la forme d’une fraction.
5 = 5/1 x = x/1 3,4 = 3,4/1
Règle 6 : Il existe des exposants fractionnaires, donc écrits sous forme de fraction. On peut transformer ces exposants par la racine d’une base avec un exposant.
Règle 7 : Il est impossible de faire des opérations sur deux nombres différents avec des exposants. Exemple : (9)2 + (3)4 = impossible. Pour résoudre ce problème, il faut avoir la même base. Exemple :
– 9^2 * 3^4
– (3^2)^2 * 3^4
– 3^(2*2) * 3^4
– 3^4 * 3^4 = 3^(4+4) = 3^8
Règle (45°,45°,90°) : Lorsque q’un triangle rectangle possède les mesures d’angles suivantes : 45°,45° et 90°, il s’agit d’un triangle isocèle alors les 2 cathètes sont isométriques. On peut alors trouver la mesure des 3 côtés si on connaît la longueur de l’hypoténuse. On doit alors avoir recours à l’algèbre.
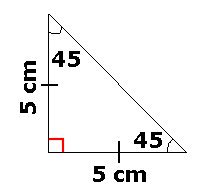
Exemple : Un triangle rectangle isocèle possède une hypoténuse de 5 cm. Trouver la mesure des 2 cathètes.
1 – Poser l’équation
a^2 + a^2 = c^2
x^2 + x^2 = hypoténuse^2
2x^2 = 5^2
2 – Résoudre l’équation
2x^2 = 5^2
2x = 5^2
2x = 25
x = 25 ÷ 2
x = 12,5 cm
Réponse : Les catètes mesure 12,5 cm.
Règle (30°,60°,90°) : Lorsque les angles du triangle rectangle sont de 30°,60° et 90° degrés, il est possible de trouver 2 mesures manquantes si l’on connaît la longueur de l’hypoténuse ou d’une cathète. Dans cette situation, la longueur de l’hypoténuse est égale à 2 fois la hauteur du triangle rectangle.
Problème : Un triangle rectangle avec les angles (30°,60°,90°) a une hypoténuse de 10 cm . Quelle est la longueur des deux autres côtés?
1- Identifier quelles sont les mesures connues
Hypoténuse = 10 cm
2- Trouver la hauteur en fonction de l’hypoténuse
Si hypoténuse = 10 cm
Hauteur = (Hypoténuse) ÷ 2
Donc 10cm ÷ 2 = 5 cm
3- Identifier le côté manquant
Hauteur (cathète) = 5cm
Hypoténuse = 10cm
Cathète = ?
4- Faire la formule de Pythagore
10^2 – 5^2 = cathète
100 – 25 = cathète
√75 = √cathète
8,66cm ≈ cathète
Description et explication : C’est une règle mathématique en géométrie qui s’applique uniquement aux triangles rectangles. Si on connaît la mesure de 2 des 3 côtés d’un triangle rectangle, on peut trouver la troisième. Premièrement, un triangle rectangle est composé de 2 cathètes et d’une hypoténuse. L’hypoténuse est tout simplement le côté le plus long et il est opposé à l’angle droit. Les 2 autres côtés sont les cathètes.
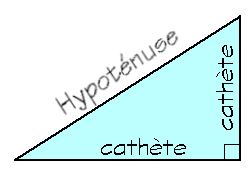
La règle de Pythagore est la suivante : Hypoténuse^2= Une cathète^2+L’autre cathète^2. On exprime souvent l’hypoténuse par la lettre « c » et les cathètes par « a » et « b ». La règle est alors écrite sous la forme de a^2 + b^2 = c^2.
Exemple d’un problème avec la relation de Pythagore :
De quelle longueur est l’hypoténuse dans le triangle rectangle suivant?
1- Identifier s’il faut trouver l’hypoténuse ou une des cathètes.
Dans ce cas si, il s’agit de l’hypoténuse, car c’est le côté le plus long.
2- Déterminer les mesures de chaque côté et poser l’équation
a = 3 3^2 + 4^2 = c^2
b = 4
c = ?
3- Résoudre l’équation
3^2 + 4^2 = c^2
9 + 16 = c^2
25 = c^2
√25 = c
5 = c
Réponse : 5 centimètres
Tout sur les maths de secondaire 3 